Доверительный интервал представляет собой диапазон значений, который с определенной вероятностью содержит истинный параметр генеральной совокупности. Рассмотрим методы его расчета и интерпретации.
Содержание
Основные понятия
| Термин | Определение |
| Доверительный уровень | Вероятность, с которой интервал содержит истинный параметр (обычно 90%, 95% или 99%) |
| Ошибка выборки | Половина ширины доверительного интервала |
| Критическое значение | Z-статистика или t-статистика, соответствующая доверительному уровню |
Формула расчета для среднего
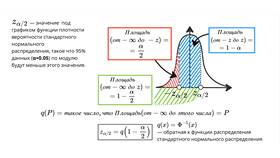
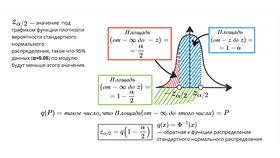
Для нормального распределения
Доверительный интервал = X̄ ± Z*(σ/√n)
- X̄ - выборочное среднее
- Z - критическое значение нормального распределения
- σ - стандартное отклонение
- n - объем выборки
Для малых выборок
Доверительный интервал = X̄ ± t*(s/√n)
- Используется t-распределение Стьюдента
- s - выборочное стандартное отклонение
- t-критерий зависит от степеней свободы (n-1)
Этапы построения
| Шаг | Действие |
| 1 | Выбор доверительного уровня (1-α) |
| 2 | Определение статистики (Z или t) |
| 3 | Расчет стандартной ошибки |
| 4 | Вычисление границ интервала |
Пример расчета для доли
- Формула: p̂ ± Z*√(p̂(1-p̂)/n)
- p̂ - выборочная доля
- Z = 1.96 для 95% доверительного уровня
- Применяется при np̂ > 5 и n(1-p̂) > 5
Факторы, влияющие на ширину интервала
- Объем выборки (обратная зависимость)
- Доверительный уровень (прямая зависимость)
- Изменчивость данных (прямая зависимость)
- Тип распределения (нормальное, t, другие)
Интерпретация результатов
Доверительный интервал 95% означает, что если многократно повторять выборку, то в 95% случаев построенные интервалы будут содержать истинное значение параметра. Это не вероятность того, что конкретный интервал содержит параметр.