Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим основные методы расчета доверительных интервалов для различных типов данных.
Содержание
Основные понятия
- Доверительная вероятность - вероятность, с которой интервал содержит истинный параметр (обычно 90%, 95% или 99%)
- Точечная оценка - выборочное среднее или пропорция
- Стандартная ошибка - мера изменчивости оценки
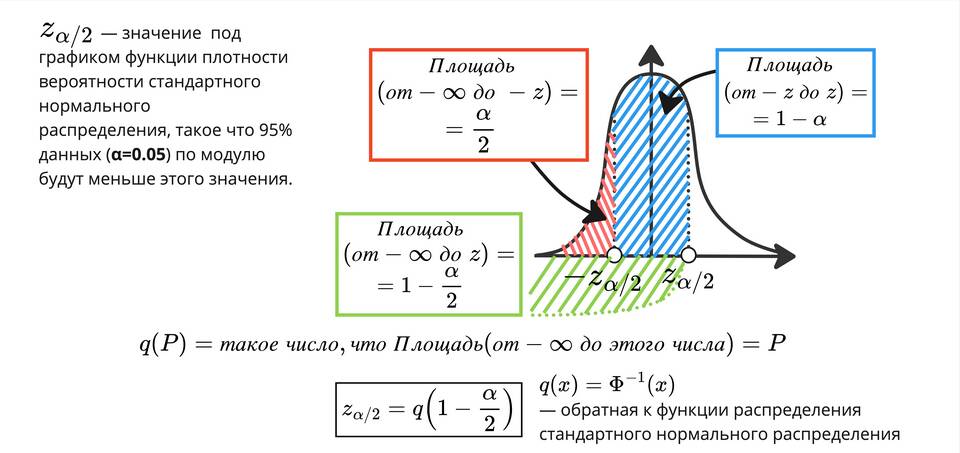
- Критическое значение - величина из распределения, соответствующая доверительной вероятности
Формулы расчета
Для среднего значения (нормальное распределение)
ДИ = x̄ ± z*(σ/√n)
- x̄ - выборочное среднее
- z - критическое значение z-распределения
- σ - стандартное отклонение
- n - объем выборки
Для пропорции
ДИ = p̂ ± z*√(p̂(1-p̂)/n)
- p̂ - выборочная пропорция
- z - критическое значение
- n - объем выборки
Критические значения
| Доверительная вероятность | z-значение |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
Этапы расчета
- Определите доверительный уровень (обычно 95%)
- Вычислите точечную оценку параметра
- Рассчитайте стандартную ошибку оценки
- Найдите критическое значение для заданного уровня доверия
- Вычислите границы интервала
Важно!
При малых выборках (n < 30) вместо z-распределения следует использовать t-распределение Стьюдента с n-1 степенями свободы. Это дает более точные результаты при работе с ограниченными данными.